August 2018 Geometry Regents

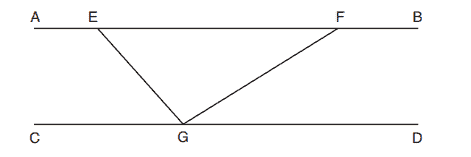
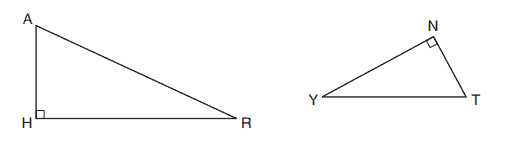1. In the diagram below, $\overline{AEFB} \| \overline{CGD}$ , and $\overline{GE}$ and $\overline{GF}$ are drawn.

If $m\angle EFG = 32^{\circ}$ and $m\angle AEG = 137^{\circ}$ , what is $m\angle EGF$ ?

(1) $11^{\circ}$
(2) $43^{\circ}$
(3) $75^{\circ}$
(4) $105^{\circ}$

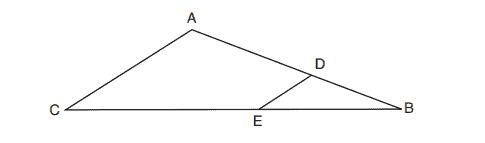
2. If $\triangle ABC$ is mapped onto $\triangle DEF$ after a line reflection and $\triangle DEF$ is mapped onto $\triangle XYZ$ after a translation, the relationship between $\triangle ABC$ and $\triangle XYZ$ is that they are always

(1) congruent and similar
(2) congruent but not similar
(3) similar but not congruent
(4) neither similar nor congruent

3. An isosceles right triangle whose legs measure 6 is continuously rotated about one of its legs to form a three-dimensional object. The three-dimensional object is a

(1) cylinder with a diameter of $6$
(2) cylinder with a diameter of $12$
(3) cone with a diameter of $6$
(4) cone with a diameter of $12$

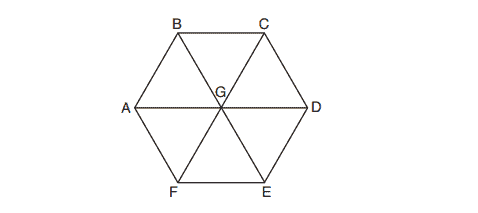
4. In regular hexagon $ABCDEF$ shown below, $\overline{AD}$ , $\overline{BE}$ , and $\overline{CF}$ all intersect at $G$ .

When $\triangle ABG$ is reflected over $\overline{BG}$ and then rotated $180^{\circ}$ about point $G$ , $\triangle ABG$ is mapped onto

(1) $\triangle FEG$
(2) $\triangle AFG$
(3) $\triangle CBG$
(4) $\triangle DEG$

5. A right cylinder is cut perpendicular to its base. The shape of the cross section is a

(1) circle
(2) cylinder
(3) rectangle
(4) triangular prism

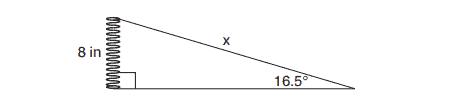
6. Yolanda is making a springboard to use for gymnastics. She has $8$ -inch-tall springs and wants to form a $16.5^{\circ}$ angle with the base, as modeled in the diagram below.

To the nearest tenth of an inch, what will be the length of the springboard, $x$ ?

(1) $2.3$
(2) $8.3$
(3) $27.0$
(4) $28.2$

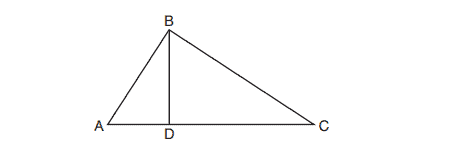
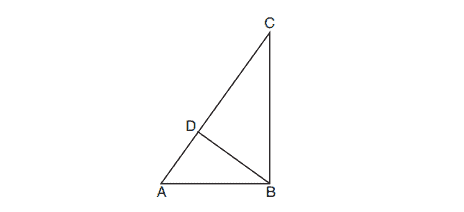
7. In the diagram below of right triangle $ABC$ , altitude $\overline{BD}$ is drawn to hypotenuse $\overline{AC}$ .

If $BD = 4$ , $AD = x - 6$ , and $CD = x$ , what is the length of $\overline{CD}$ ?

(1) $5$
(2) $2$
(3) $8$
(4) $11$

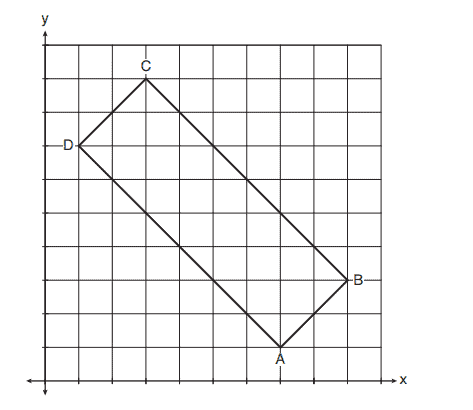
8. Rhombus $STAR$ has vertices $S(-1,2)$ , $T(2,3)$ , $A(3,0)$ , and $R(0,-1)$ . What is the perimeter of rhombus $STAR$ ?

(1) $\sqrt{34}$
(2) $4\sqrt{34}$
(3) $\sqrt{10}$
(4) $4\sqrt{10}$

9. In the diagram below of $\triangle HAR$ and $\triangle NTY$ , angles $H$ and $N$ are right angles, and $\triangle HAR \sim \triangle NTY$ .

If $AR = 13$ and $HR = 12$ , what is the measure of angle $Y$ , to the nearest degree?

(1) $23^{\circ}$
(2) $25^{\circ}$
(3) $65^{\circ}$
(4) $67^{\circ}$

10. In the diagram below, $\overline{AKS}$ , $\overline{NKC}$ , $\overline{AN}$ , and $\overline{SC}$ are drawn such that $\overline{AN} \cong \overline{SC}$ .

Which additional statement is sufficient to prove $\triangle KAN \cong \triangle KSC$ by AAS?

(1) $\overline{AS}$ and $\overline{NC}$ bisect each other
(2) $K$ is the midpoint of $\overline{NC}$
(3) $\overline{AS} \perp \overline{CN}$
(4) $\overline{AN} \| \overline{SC}$

11. Which equation represents a line that is perpendicular to the line represented by $y = \dfrac{2}{3}x + 1$ ?

(1) $3x + 2y = 12$
(2) $3x - 2y = 12$
(3) $y = \dfrac{3}{2}x + 2$
(4) $y = -\dfrac{2}{3}x + 4$

12. In the diagram of $\triangle ABC$ below, points $D$ and $E$ are on sides $\overline{AB}$ and $\overline{CB}$ repectively, such that $\overline{DE} \| \overline{AC}$ .

If $AB$ is $3$ more than $DB$ , $AB = 14$ , and $CB = 21$ , what is the length of $\overline{AD}$ ?

(1) $6$
(2) $8$
(3) $9$
(4) $12$

13. Quadrilateral $\text{[math]}$ has both pairs of opposite sides congruent and parallel. Which statement about quadrilateral $\text{[math]}$ is always true?

(1) $\overline{MT} \cong \overline{AH}$
(2) $\overline{MT} \perp \overline{AH}$
(3) $\angle MHT \cong \angle ATH$
(4) $\angle MAT \cong \angle MHT$

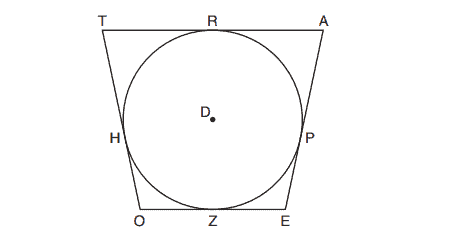
14. In the figure shown below, quadrilateral $TAEO$ is circumscribed around circle $D$ . The midpoint of $\overline{TA}$ is $R$ , and $\overline{HO} \cong \overline{PE}$ .

If $AP = 10$ and $EO = 12$ , what is the perimeter of quadrilateral $TAEO$ ?

(1) $56$
(2) $64$
(3) $72$
(4) $76$

15. The coordinates of the endpoints of directed line segment $ABC$ are
$A(-8,7)$ and $C(7,-13)$ . If $AB:BC = 3:2$ , the coordinates of $B$ are

(1) ( $1, -5$ )
(2) ( $-2, -1$ )
(3) ( $-3, 0$ )
(4) ( $3, -6$ )

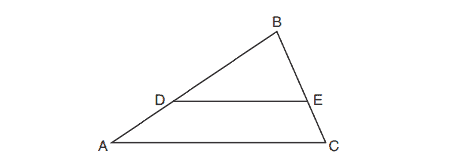
16. In triangle $ABC$ , points $D$ and $E$ are on sides $\overline{AB}$ and $\overline{BC}$ , respectively, such that $\overline{DE} \| \overline{AC}$ , and $AD:DB = 3:5$ .

If $DB = 6.3$ and $AC = 9.4$ , what is the length of $\overline{DE}$ , to the nearest tenth?

(1) $3.8$
(2) $5.6$
(3) $5.9$
(4) $15.7$

17. In the diagram below, rectangle $ABCD$ has vertices whose coordinates are $A(7,1)$ , $B(9,3)$ , $C(3,9)$ , and $D(1,7)$ .

Which transformation will not carry the rectangle onto itself?

(1) a reflection over the line $y = x$
(2) a reflection over the line $y = -x + 10$
(3) a rotation of $180^{\circ}$ about the point ( $6,6$ )
(4) a rotation of $180^{\circ}$ about the point ( $5,5$ )

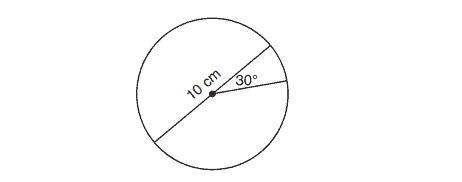
18. A circle with a diameter of $10$ cm and a central angle of $30^{\circ}$ is drawn below.

What is the area, to the nearest tenth of a square centimeter, of the sector formed by the $30^{\circ}$ angle?

(1) $5.2$
(2) $6.5$
(3) $13.1$
(4) $26.2$

19. A child’s tent can be modeled as a pyramid with a square base whose sides measure $60$ inches and whose height measures $84$ inches. What is the volume of the tent, to the nearest cubic foot?

(1) $35$
(2) $58$
(3) $82$
(4) $175$

20. In the accompanying diagram of right triangle $ABC$ , altitude $\overline{BD}$ is drawn to hypotenuse $\overline{AC}$ .

Which statement must always be true?

(1) $\dfrac{AD}{AB} = \dfrac{BC}{AC}$
(2) $\dfrac{AD}{AB} = \dfrac{AB}{AC}$
(3) $\dfrac{BD}{BC} = \dfrac{AB}{AD}$
(4) $\dfrac{AB}{BC} = \dfrac{BD}{AC}$

21. An equation of circle $O$ is $x^{2} + y^{2} + 4x - 8y = -16$ . The statement that best describes circle $O$ is the

(1) center is ( $2,4$ ) and is tangent to the $x$ -axis
(2) center is ( $2,4$ ) and is tangent to the $y$ -axis
(3) center is ( $2,4$ ) and is tangent to the $x$ -axis
(4) center is ( $2,4$ ) and is tangent to the $y$ -axis

22. In $\triangle ABC$ , $\overline{BD}$ is the perpendicular bisector of $\overline{ADC}$ . Based upon this information, which statements below can be proven?

I. $\overline{BD}$ is a median.
II. $\overline{BD}$ bisects $\angle ABC$ .
III. $\triangle ABC$ is isosceles.

(1) I and II, only
(2) I and III, only
(3) II and III, only
(4) I, II, and III

23. Triangle $RJM$ has an area of $6$ and a perimeter of $12$ . If the triangle is dilated by a scale factor of $3$ centered at the origin, what are the area and perimeter of its image, triangle $R'J'M'$ ?

(1) area of $9$ and perimeter of $15$
(2) area of $18$ and perimeter of $36$
(3) area of $54$ and perimeter of $36$
(4) area of $54$ and perimeter of $108$

24. If $sin (2x + 7)^{\circ} = cos (4x - 7)^{\circ}$ , what is the value of $x$ ?

(1) $7$
(2) $15$
(3) $21$
(4) $30$