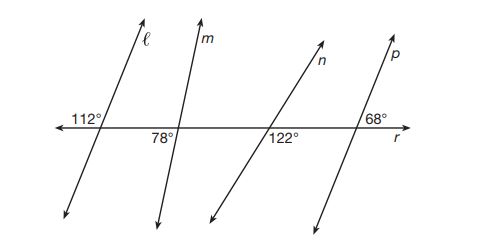
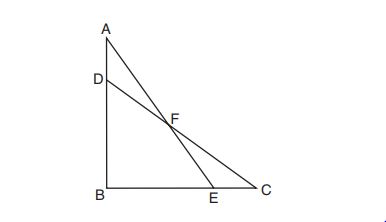
1. In the diagram below, lines ,
,
, and
intersect line
.
Which statement is true?
(1)
(2)
(3)
(4)
2. Which transformation would not always produce an image that would be congruent to the original figure?
(1) translation
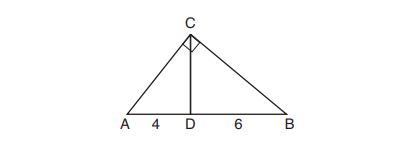
(2) dilation
(3) rotation
(4) reflection
3. If an equilateral triangle is continuously rotated around one of its medians, which -dimensional object is generated?
(1) cone
(2) pyramid
(3) prism
(4) sphere
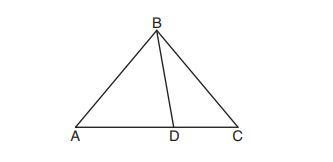
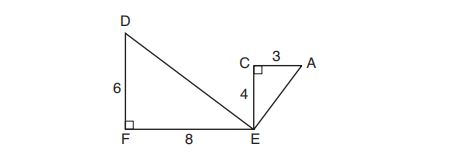
4. In the diagram below, , and
.
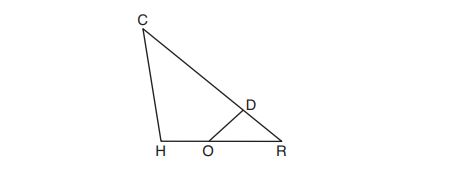
Which statement is true?
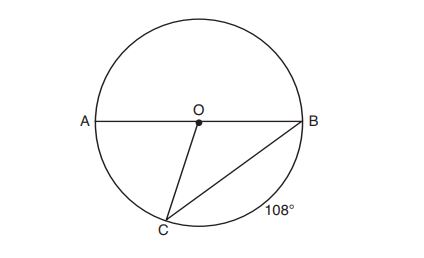
(1) is obtuse
(2) is isosceles
(3)
(4) is scalene
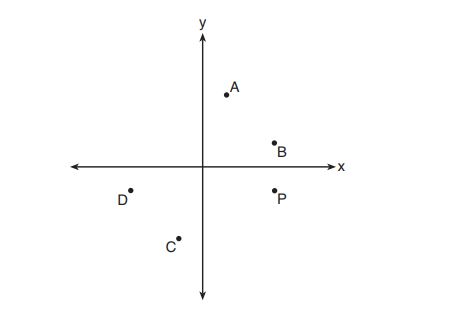
5. Which point shown in the graph below is the image of point after a counterclockwise rotation of
about the origin?
(1)
(2)
(3)
(4)
6. In , where
is a right angle,
. What is
?
(1)
(2)
(3)
(4)
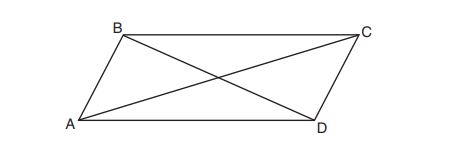
7. Quadrilateral with diagonals
and
is shown in the diagram below.
Which information is not enough to prove is a parallelogram?
(1) and
(2) and
(3) and
(4) and
8. An equilateral triangle has sides of length . To the nearest tenth, what is the height of the equilateral triangle?
(1)
(2)
(3)
(4)
9. Given: , and
What is a correct sequence of similarity transformations that shows ?
(1) a rotation of degrees about point
followed by a horizontal translation
(2) a counterclockwise rotation of degrees about point
followed by a horizontal translation
(3) a rotation of degrees about point
followed by a dilation with a scale factor of
centered at point
(4) a counterclockwise rotation of degrees about point
followed by a dilation with a scale factor of
centered at point
10. In the diagram of right triangle ,
intersects hypotenuse
at
.
If and
, which length of
makes
?
(1)
(2)
(3)
(4)
11. Segment is the perpendicular bisector of
at
. Which pair of
segments does not have to be congruent?
(1)
(2)
(3)
(4)
12. In triangle is on
, and
is on
so that
.
If , and
, what is the length of
?
(1)
(2)
(3)
(4)
13. The cross section of a regular pyramid contains the altitude of the pyramid. The shape of this cross section is a
(1) circle
(2) square
(3) triangle
(4) rectangle
14. The diagonals of rhombus intersect at
. If the equation of the line that contains diagonal
is
, what is the equation of a line that contains diagonal
?
(1)
(2)
(3)
(4)
15. The coordinates of vertices and
of
are
and
. If the area of
is
square units, what could be the coordinates of point
?
(1) ()
(2) ()
(3) ()
(4) ()
16. What are the coordinates of the center and the length of the radius of the circle represented by the equation ?
(1) center () and radius
(2) center () and radius
(3) center () and radius
(4) center () and radius
17. The density of the American white oak tree is kilograms per cubic meter. If the trunk of an American white oak tree has a circumference of
meters and the height of the trunk is
meters, what is the approximate number of kilograms of the trunk?
(1)
(2)
(3)
(4)
18. Point is on the directed line segment from point
to point
and divides the segment in the ratio
. What are the coordinates of point
?
(1) ()
(2) ()
(3) ()
(4) ()
19. In circle , diameter
, chord
, and radius
are drawn, and the measure of arc
is
.
Some students wrote these formulas to find the area of sector :
Amy
Beth
Carl
Dex
Which students wrote correct formulas?
(1) Amy and Dex
(2) Beth and Carl
(3) Carl and Amy
(4) Dex and Beth
20. Tennis balls are sold in cylindrical cans with the balls stacked one on top of the other. A tennis ball has a diameter of cm. To the nearest cubic centimeter, what is the minimum volume of the can that holds a stack of
tennis balls?
(1)
(2)
(3)
(4)
21. Line segment , whose endpoints are (
) and (
), is the image of
after a dilation of
centered at the origin. What
is the length of ?
(1)
(2)
(3)
(4)
22. Given: and
shown in the diagram below with
Which statement is needed to prove using
?
(1)
(2)
(3)
(4)
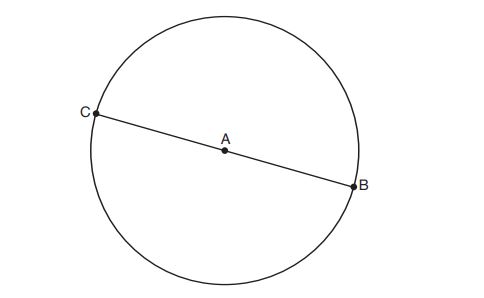
23. In the diagram below, is the diameter of circle
.
Point , which is unique from points
and
, is plotted on circle
. Which statement must always be true?
(1) is a right triangle.
(2) is an isosceles triangle.
(3) and
are similar triangles.
(4) and
are congruent triangles.
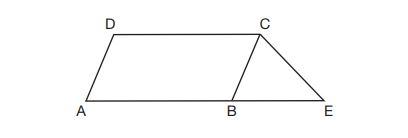
24. In the diagram below, is a parallelogram,
is extended through
to
, and
is drawn.
If and
, what is
?
(1)
(2)
(3)
(4)