1. A certain human red blood cell has a diameter of meters. Which expression represents this diameter, in meters, in scientific notation?
A.
B.
C.
D.
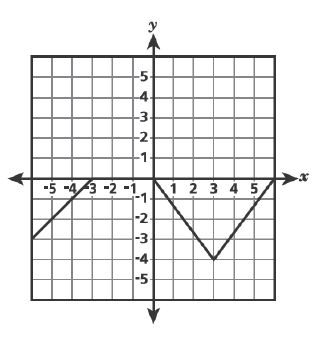
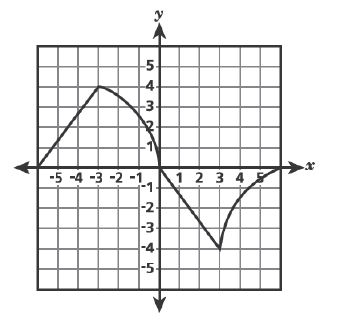
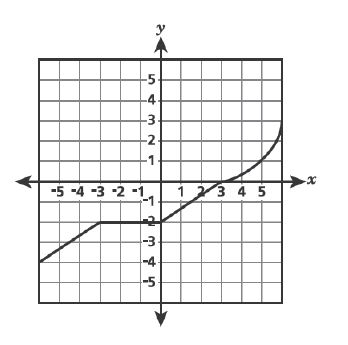
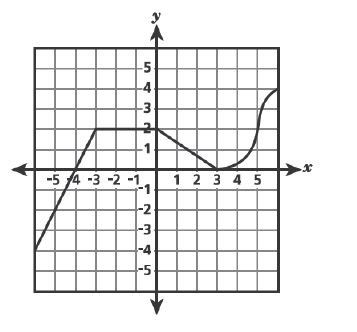
2 .A function has the following properties:
– It is increasing and linear when the value of is between
and
.
– It remains constant when the value of is between
and
.
-It is decreasing and linear when the value of is between
and
.
– It is increasing and nonlinear when the value of is between
and
.
Which graph best represents this function?
A.
B.
C.
D.
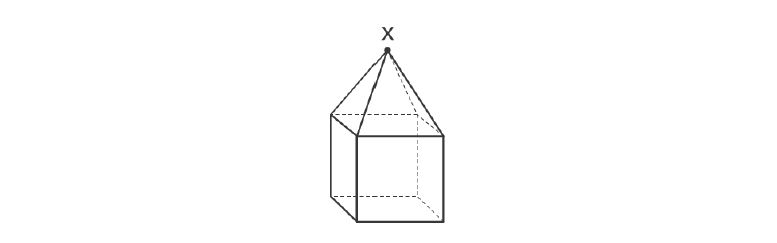
3. The figure shown below consists of a square pyramid on top of a cube. A vertical plane passes through point and is perpendicular to the bases of both shapes, slicing the figure into equal halves.
What shape is created by the intersection of the vertical plane and these three-dimensional shapes?
A. square
B. triangle
C. hexagon
D. pentagon
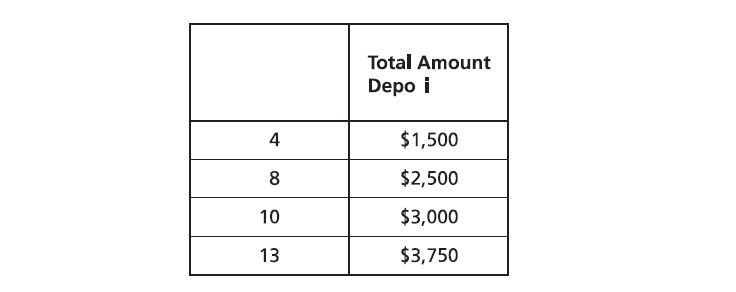
4. Ms. Gibson made an initial deposit of when opening a bank account. After the initial deposit, she deposited the same amount of money each month. The table below shows the total amount of money, a, she deposited into the account after a certain number of months, t, since opening it.
Which equation models the relationship between a and t?
A.
B.
C.
D.
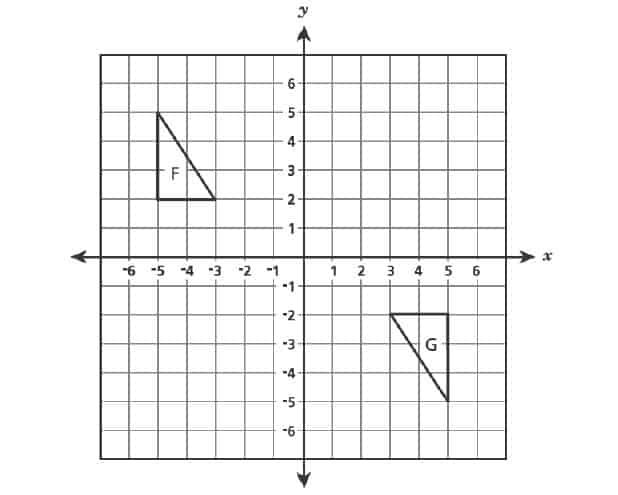
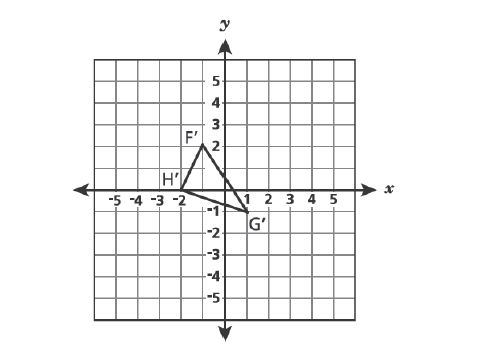
5. Triangle and triangle
are shown below.
Which sequence does not transform triangle to triangle
?
A. a clockwise rotation about the origin
B. a counterclockwise rotation about the origin
C. a reflection over the -axis then a reflection over the
-axis
D. a reflection over the -axis and then a
clockwise rotation about the origin
6. Which statement explains the type of function that is represented by the equation ?
A. The function is linear because it contains more than one term.
B. The function is linear because the variable is raised to the second power.
C. The function is nonlinear because it contains more than one term.
D. The function is nonlinear because the variable is raised to the second power.
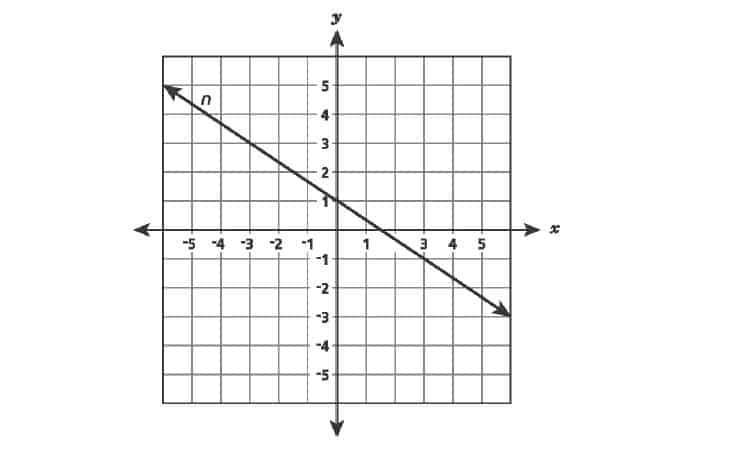
7. Line is shown on the grid below.
Line will be graphed on the same grid. The only solution to the system of linear equations formed by lines
and
occurs when
and
.Which equation could represent line
?
A.
B.
C.
D.
8. The table represents linear Function .
The equation represents Function
.
Which statement is true?
A. The rate of change of Function is less than the rate of change of Function
because
.
B. The rate of change of Function is less than the rate of change of Function
because
.
C. The rate of change of Function is greater than the rate of change of Function
because
D. The rate of change of Function is greater than the rate of change of Function
because
9. What is the solution to the equation shown below?
A.
B.
C.
D.
10. A company performed power tests on a set of batteries of the same type. The company determined that the equation , where
is the number of hours of use and
is the perfect of battery power remaining, models the battery life. Based on the equation, what is the best prediction of the percent of remaining power for a battery after
hours of use?
A.
B.
C.
D.
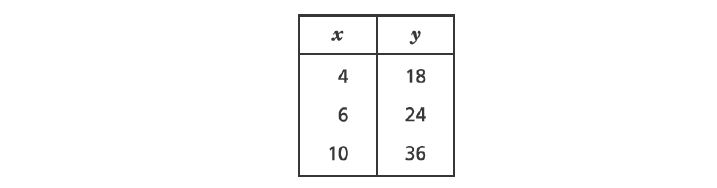
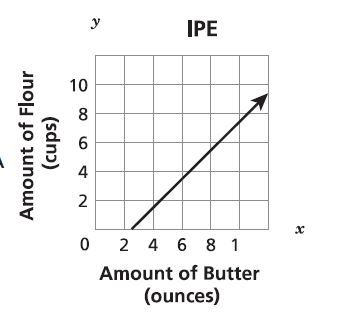
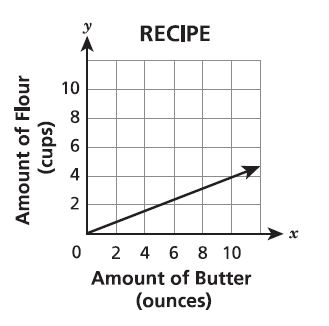
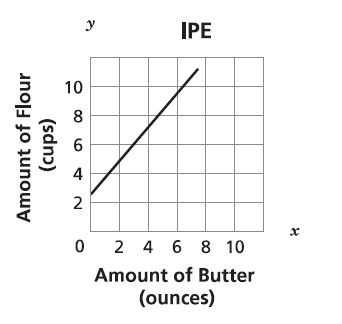
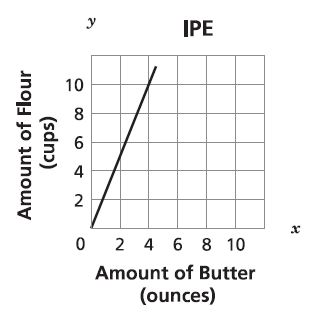
15. A cook uses cups of flour for each ounce of butter in a recipe. Which graph represents the relationship between the amount of flour and the amount of butter in the recipe?
A.
B.
C.
D.
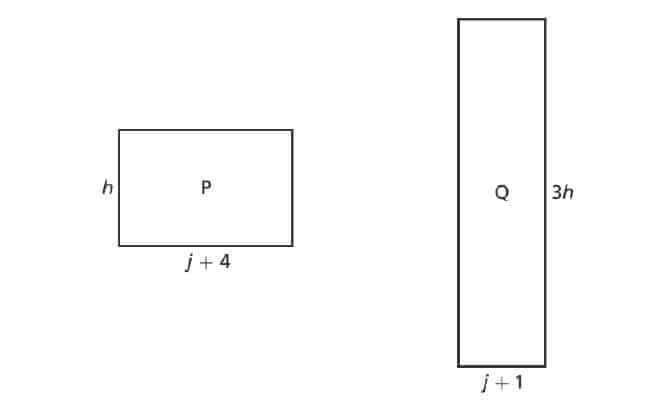
18. Two rectangles are shown below. Rectangle has a perimeter of
inches. Rectangle
has a perimeter of [/latex]30[/latex] inches.
What are the values of and
?
A. and
B. and
C. and
D. and
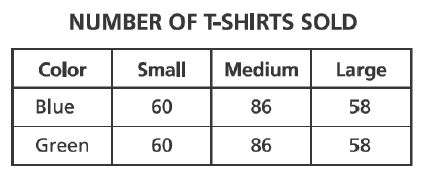
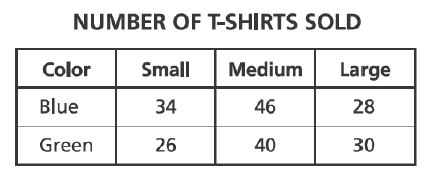
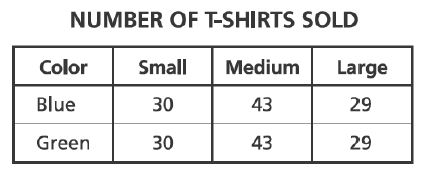
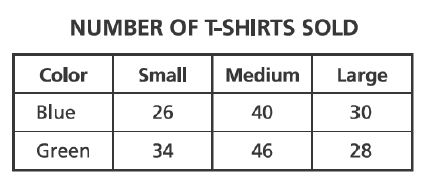
19. A school club had a T-shirt sale to raise money. After the sale, an inventory showed that blue T-shirts and
green T-shirts had been sold. The sizes of these T-shirts included
small,
medium, and
large. Which table correctly represents these data?
A.
B.
C.
D.
20. The vertices of a triangle are located at , and
. A sequence of transformations to triangle
results in triangle
, as shown below.
Which sequence of transformations to triangle results in triangle
?
A. a clockwise rotation about the origin, then a dilation by a scale factor of
with a center of dilation at the origin
B. a counterclockwise rotation about the origin, then a dilation by a scale factor of
with a center of dilation at the origin
C. a counterclockwise rotation about the origin, then a dilation by a scale factor of
with a center of dilation at the origin
D. a clockwise rotation about the origin, then a dilation by a scale factor of
with a center of dilation at the origin
24. What is the value of in the equation shown below?
A.
B.
C.
D.
25. Which set of ordered pairs represents a function?
A.
B.
C.
D.
26. A parallelogram with vertices at and
is reflected over the
-axis. Which vertex of the parallelogram will have the same
-coordinate before and after the reflection?
A.
B.
C.
D.
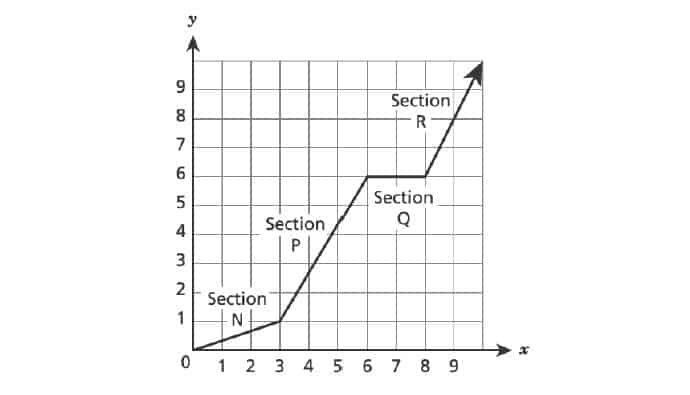
27. The graph of a function is shown below.
Which statement is true about a section of the graph?
A. In Section , the function is linear and decreasing.
B. In Section , the function is linear and increasing.
C. In Section , the function is nonlinear and decreasing.
D. In Section , the function is nonlinear and increasing.
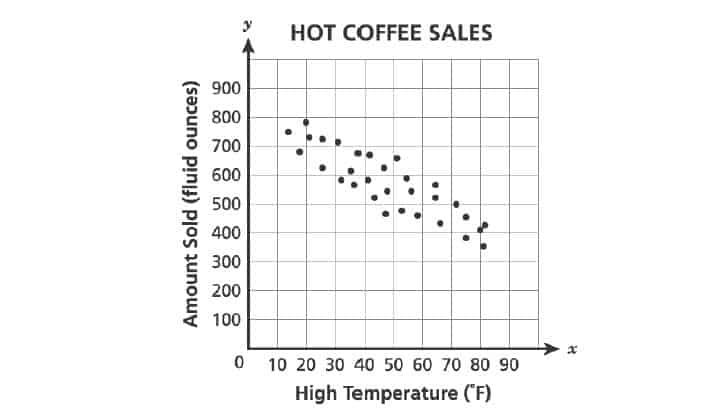
28. The owner of a coffee shop compared the amount of hot coffee per day, in fluid ounces, sold and the daily high temperature, in degrees Farenheit, per day. Her data are shown in the scatter plot below.
If these data are modeled by the line , which statement best describes a valid prediction the owner could make?
A. For each temperature increase of F, the shop can expect to sell about
fluid ounces more hot coffee.
B. For each temperature decrease of F, the shop can expect to sell about
fluid ounces more hot coffee.
C. On a day with a high temperature of F, the shop can expect to sell about
fluid ounces of hot coffee.
D. On a day with a high temperature of F, the shop can expect to sell about
fluid ounces of hot coffee.
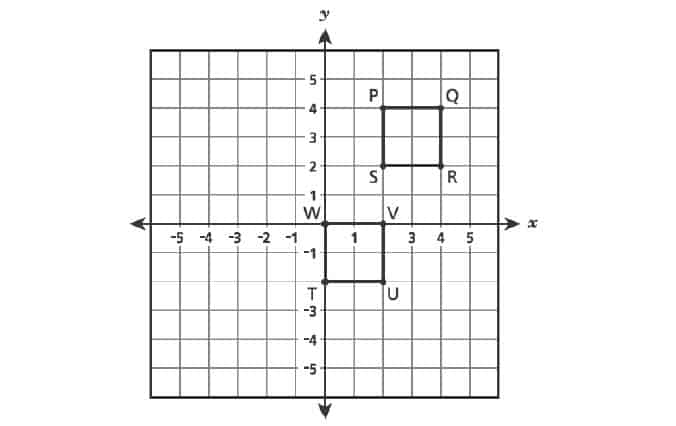
29. Squares and
are shown below.
Which sequence of transformation of square shows that square
is congruent to square
?
A. a translation units up and
units to the right, then a reflection over the
-axis
B. a translation units up and
units to the right, then a reflection over the
-axis
C. a translation units down and
units to the left, then a reflection over the
-axis
D. a translation units down and
units to the left, then a reflection over the
-axis
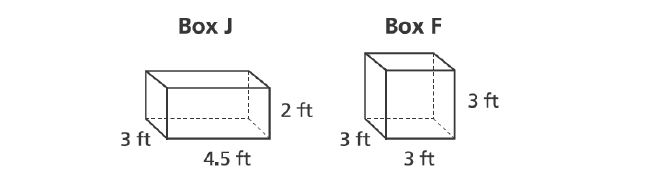
30. Two types of shipping boxes are shown below.
What is the difference in the surface areas, in square feet, of the two boxes?
A.
B.
C.
D.
31. Which expression is equivalent to ?
A.
B.
C.
D.
32. The object below was made by placing a cone on top of a cylinder. The base of the cone is congruent to the base of the cylinder.
What is the volume, in cubic centimeters, of the object?
A.
B.
C.
D.
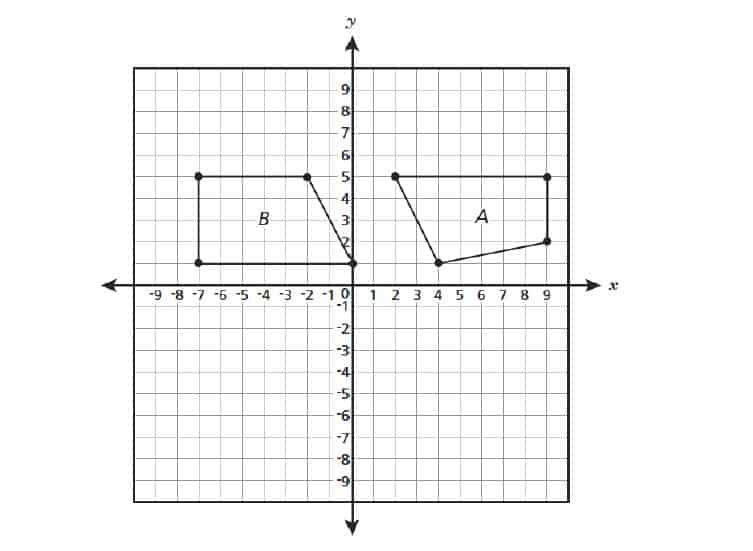
34. Lily wants to define a transformation (or series of transformations) using only rotation, reflections, or translations that takes Figure to Figure
.
Which statement about the transformation that Lily wants to define is true?
A. It can be defined with two reflections.
B. It can be defined with one rotation and one translation.
C. It cannot be defined because Figure A and Figure B are not congruent.
D. It cannot be defined because the longest side of Figure B is on the bottom.
35. What is the solution to the system equations below?
A.
B.
C.
D.
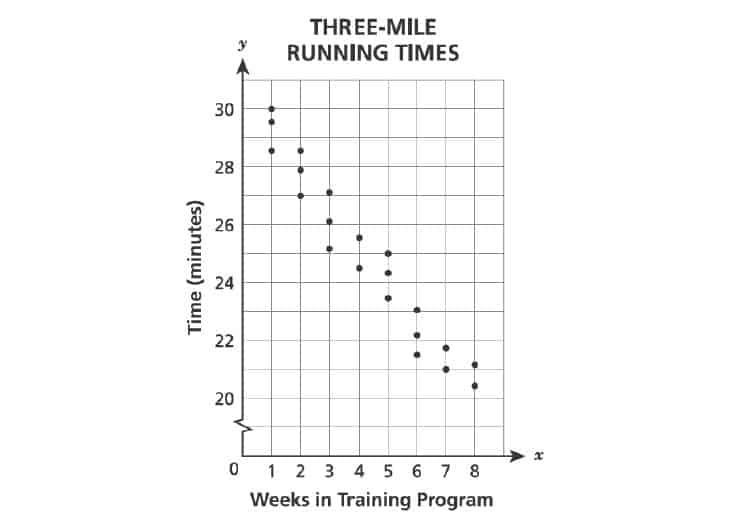
36. As part of a training program for a triathlon, Marcie completes a three-mile run a few times a week. The scatter plot below shows the times in which Marcie completes this run for each week that she has been in the training program.
Based on these data, which statement best describes the relationship between the number of weeks Marcie has been in the training program and her running times.
A. There is a negative linear association with no outliers.
B. There is a negative linear association with one outlier.
C. There is a positive linear association with no outliers.
D. There is a positive linear association with one outlier.
37. What is the solution to the equation below?
A.
B.
C.
D.
38. Which statement best explains whether these ordered pairs represent a function?
A. The ordered pairs represent a function because no output values are repeated.
B. The ordered pairs represent a function because each output value is greater than each input value.
C. The ordered pairs do not represent a function because one input value has two different output values.
D. The ordered pairs do not represent a function because the difference between the input and output of each ordered pair is not the same.
39. The amount of revenue in dollars, , that Jason receives from selling
posters is given by the equation
. The cost of producing
posters is given by the equation
. How many posters does Jason need to sell so that the cost and revenue are equal?
A.
B.
C.
D.
40. A car travelled miles in
minutes. The car traveled at a constant speed. If the car continues to travel at this rate, which equation can be used to determine
, the total number of miles the car will travel, in
hours?
A.
B.
C.
D.
42. The mass of a dust particle is approximately kilograms and the mass of an electron is
kilograms. Approximately how many electrons have the same mass as one dust particle?
A.
B.
C.
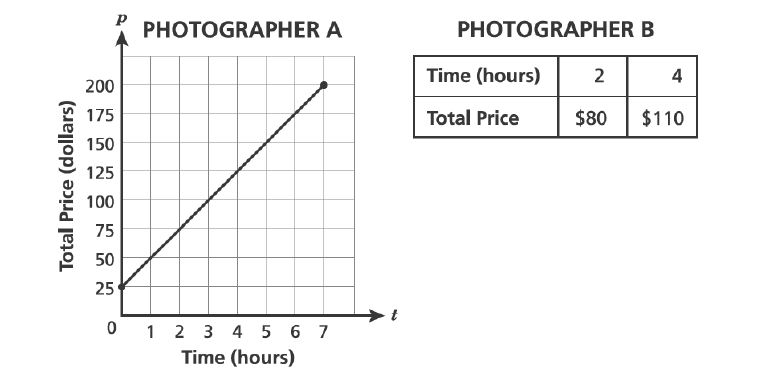
D.
43. Two photographers offer different pricing plans for their services. The graph below models the prices Photographer charges. The table below shows the prices Photographer
charges. Each photographer charges a one-time equipment fee and an hourly rate.
Which statement about the two pricing plans is true?
A. Photographer A charges per hour more than Photographer B.
B. Photographer charges
per hour more than Photographer
.
C. Photographer A’s equipment fee is lee than Photographer B’s.
D. Photographer B’s equipment fee is $ less than Photographer A’s.
44. Acute is rotated about a point and then dilated by a scale factor of
to produce
. Which statement correctly compares
to
?
A. The angle measures and side lengths of are half the size of those of
.
B. The angle measures of are the same as those of
, but the side lengths of
are half the size of those
.
C. The angle measures of are the same as those of
, but the side lengths of
are twice the size of those of
.
D. The angle measures of depend on the angle rotation, but the side lengths of
are half the size of those of
.
45. Which expression is equivalent to and written in scientific notation?
A.
B.
C.
D.
46. The points and
lie on the graph of a linear function of
. Which point also lies on the graph of this function?
A.
B.
C.
D.
47. What value for the constant, , in the equation shown below will result in an infinite number of solutions?
A.
B.
C.
D.
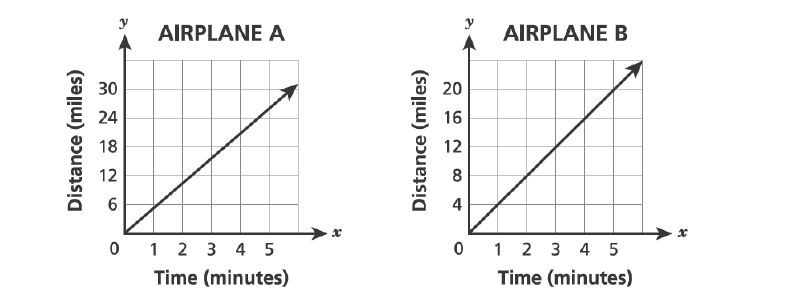
50. The graphs below show the relationship between elapsed time and distance traveled by airplane and airplane
after each airplane reaches its cruising speed.
Airplane C is traveling at a different cruising speed. The equation can be used to determine
, the number of miles traveled by airplane
in
minutes. Which statement accurately compares the cruising speed of airplane
to airplanes
and
?
A. The cruising speed of airplane C is less than the cruising speeds of both airplanes A and B.
B. The cruising speed of airplane C is greater than the cruising speeds of both airplanes A and B.
C. The cruising speed of airplane C is greater than the cruising speed of airplane A and less than the cruising speed of airplane B.
D. The cruising speed of airplane C is less than the cruising speed of airplane A and greater than the cruising speed of airplane B.
51. Two transformations are performed on a figure on a coordinate plane. The first transformation is a translation units to the left. Which second transformation will result in an image that is similar to, but not congruent to, the original figure?
A. a clockwise rotation of about the center
B. a clockwise rotation of about the center
C. a dilation by a scale factor of with the origin as the center of dilation
D. a dilation by a scale factor of with the origin as the center of dilation