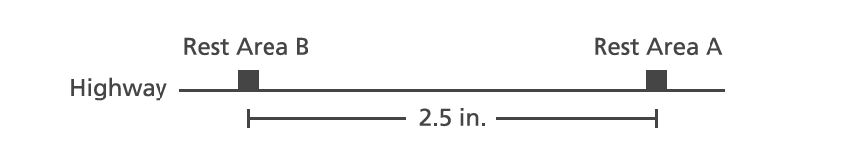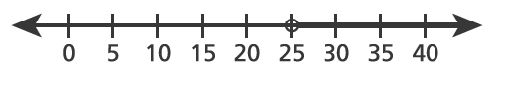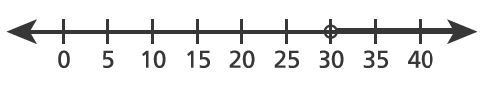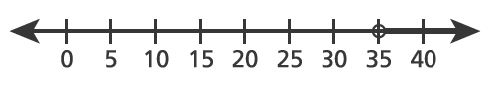1. Point is shown on the number line below.
The distance between point and point
is
units. Which number could represent point
?
A.
B.
C.
D.
2. Ms. Gartland bought number of shirts for the new members of her chorus. The cost for
number of shirts, including
shipping, was
. Each shirt cost
. There was no sales tax on this purchase. Which equation could be used to find
?
A.
B.
C.
D.
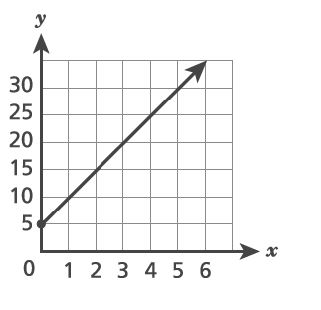
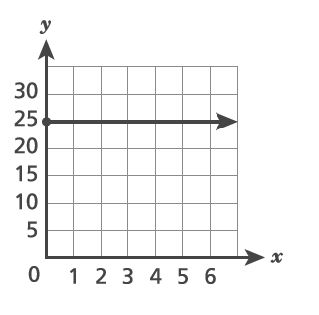
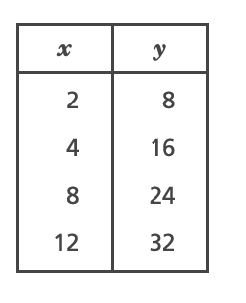
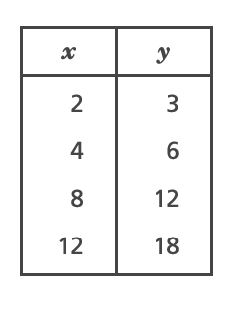
3. Which representation shows a proportional relationship between and
?
A.
B.
C.
D.
4. Every five years in March, the population of a certain town is recorded. In 1995, the town had a population of people. From
to
, the population increased by
. From 2000 to 2005, the population decreased by
. What was the town’s population in
?
A.
B.
C.
D.
9. The measure of one side of a square is inches long. Which pair of expressions both represent the perimeter of this square?
A.
and
B.
and
C.
and
D.
and
10. Which expression has the same value as ?
A.
B.
C.
D.
11. Winston needs at least signatures from students in his school before he can run for class president. He has
signatures already. He and two of his friends plan to get the remaining signatures during lunch. If each person gets the same number of signatures, which inequality can Winston use to determine the minimum number of signatures each person should get so he can run for class president?
A.
B.
C.
D.
12. In the morning, a farm worker packed pints of strawberries every
minutes. In the afternoon, she packed
pints of strawberries every
minutes. What was the difference between her morning and afternoon packing rates, in pints per hour?
A.
B.
C.
D.
13. Which expression makes the equation true for all values of ?
(_?_)
A.
B.
C.
D.
14. Which number is equivalent to ?
A.
B.
C.
D.
15. Mr. Santino needs a total of forks for his restaurant. He currently has
forks. If each set has
forks, what is the minimum number of sets of forks he should buy?
A.
B.
C.
D.
16. If the expression below has a positive value, which inequality represents all possible values of in the expression?
A.
B.
C.
D.
19. Jensen stopped at the rest area along the side of the highway. His map, shown below, has a scale of
inch to
miles.
Jensen planned to stop at rest area next. What is the actual distance, in miles, between the two rest areas?
A.
B.
C.
D.
20. Which statement describes the decimal equivalent of ?
A. It is a decimal with a repeating digit of .
B. It is a decimal with repeating digits of .
C. It is a decimal that terminates after decimal places.
D. It is a decimal that terminates after decimal places.
21. Which expression is equivalent to the expression shown below?
A.
B.
C.
D.
22. Leanne collects data throughout the basketball season and uses these data to determine the probabilities of different teams playing in the league championship game. The probabilities for her four favorite teams playing in the championship game are shown below.
– Tigers:
– Redbirds:
– Bulldogs:
– Titans:
Which of these teams is least likely to play in the championship game?
A. Tigers
B. Redbirds
C. Bulldogs
D. Titans
25. The initial balance of a savings account was . After which transactions will the balance of the savings account be the same as the initial balance?
A. a withdrawal of $ followed by a deposit of $
B. a deposit of $ followed by a withdrawal of $
C. a withdrawal of $ followed by a deposit of $
D. a deposit of $ followed by a withdrawal of $
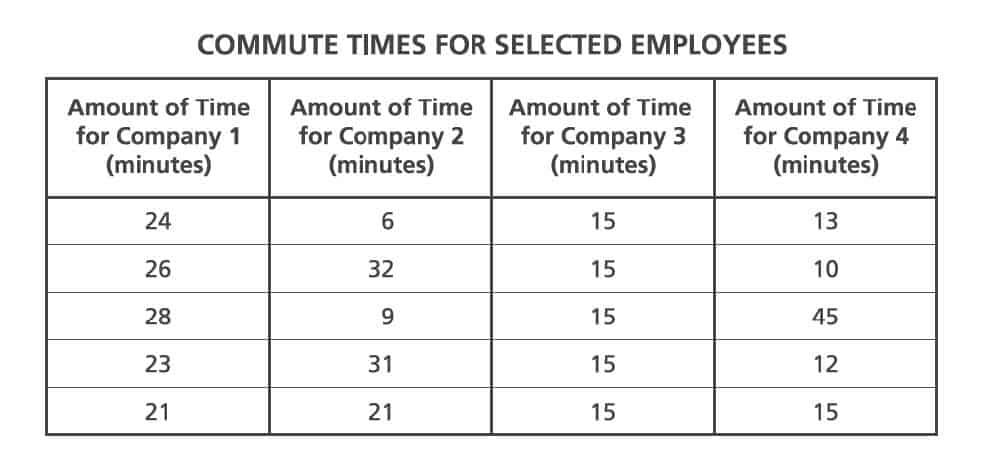
26. A researcher surveyed five randomly selected employees from each of four different companies about their daily commutes to work. The table shows the commute times for the surveyed employees.
Based on the data, which company most likely has the longest average commute time per employee?
A. Company
B. Company
C. Company
D. Company
27. In a scale drawing of an apartment, centimeter represents
feet. If the length of the kitchen is
cm on the scale drawing, what is the actual length, in feet, of the kitchen?
A.
B.
C.
D.
28. A passenger train has tickets available for window seats and
aisle seats. The next person to buy a ticket will be randomly assigned to one of those seats. What is the probability that the next person will be assigned to an aisle seat?
A.
B.
C.
D.
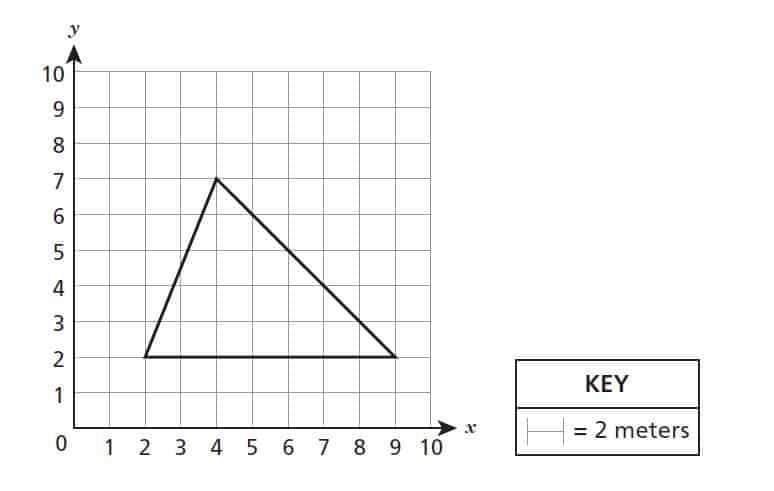
32. The scale drawing of a field in the shape of a triangle is shown below.
What is the actual area, in square meters, of this field?
A.
B.
C.
D.
33. A vehicle uses a gallons of gasoline to travel
miles. At this rate, how many miles can the vehicle travel per gallon of gasoline?
A.
B.
C.
D.
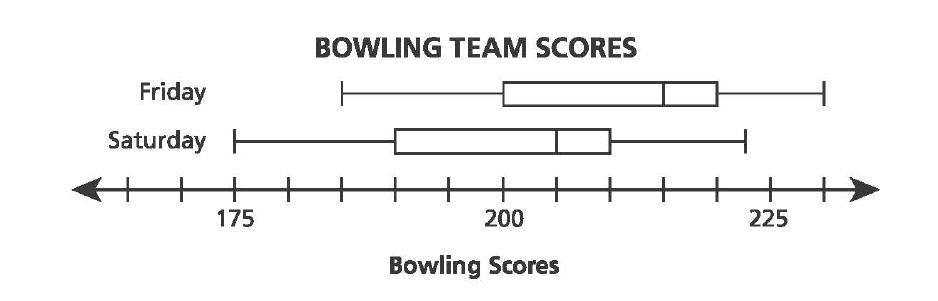
34. A bowling team participates in a two-day tournament and records the scores for each team member on both days. The scores for both days are represented by the box plots below.
Which conclusion can be drawn from the box plots?
A. The scores on Friday and the scores on Saturday have the same median and interquartile range.
B. The scores on Friday have a greater median and a greater interquartile range than the scores on Saturday.
C. The scores on Friday have a greater interquartile range than the scores on Saturday, but both data sets have the same median.
D. The scores on Friday have a greater median than the scores on Saturday, but both data sets have the same interquartile range.
35. Which expression is equivalent to ?
A.
B.
C.
D.
36. Jeanette purchased a concert ticket on a web site. The original price of the ticket was . She used a coupon code to receive a
discount. The web site applied a
service fee to the discounted price. Jeanette’s ticket was less than the original price by what percent?
A.
B.
C.
D.
37. A seventh grade English Language Arts teacher wants to order books for all the seventh grade classes. He wants to determine the favorite type of book among the seventh grade students. Which sample would be the most appropriate for this survey?
A. girls in each of his classes
B. every fifth student in the seventh grade
C. out of
students in his middle school
D. all of the boys in one of his seventh grade classes
38. The amount of money in a bank account increased by over the last year. If the amount of money at the beginning of the year is represented by
, which expression represents the amount of money in the bank account after the increase?
A.
B.
C.
D.
39. Kiyo used wire fencing to form a border around a circular region in his back yard. If the radius of the circular region was yards, what was the total length of the border, rounded to the nearest tenth of a yard?
A.
B.
C.
D.
40. A triangle has side lengths of centimeters,
centimeters, and
centimeters. Which expression represents the perimeter, in centimeters, of the triangle?
A.
B.
C.
D.
41. Carl wants to buy a television that costs , including taxes. To pay for the television, he will use a payment plan that requires him to make a down payment of
, and then pay
each month for
months. What is the percent increase from the original cost of the television to the cost of the television using the payment plan?
A.
B.
C.
D.
42. Yolanda participated in a walkathon in which each kilometer walked raised for charity. Her goal was to raise more than
on Saturday and Sunday. She raised
on Saturday. Which graph shows all the distances, in kilometers, that Yolanda could have walked on Sunday to reach her goal?
A.
B.
C.
D.
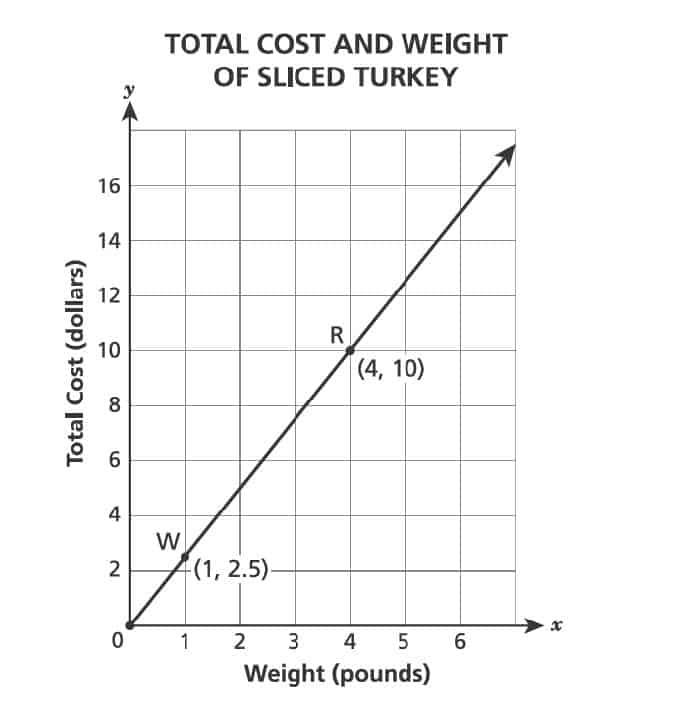
43. A grocery store sells sliced turkey. The graph shows the relationship between the weight of the sliced turkey and the total cost of the sliced turkey. Two points, and
, are labeled on the graph shown below.
Which statement about the graph is true?
A. Point means that the unit rate is
per pound.
B. Point means that the unit rate is
pounds per dollar.
C. Point means that the unit rate is
per pound.
D. Point means that the unit rate is
pounds per dollar.
44. An item with an original price of dollars is on sale at a
discount. Which expression is not equivalent to the price of the item with the discount?
A.
B.
C.
D.
45. A circle has a diameter of units. What is the area of the circle to the nearest hundredth of a square unit?
A.
B.
C.
D.
46. The width of a rectangle is inches. The length of the rectangle is twice its width. What is the perimeter of the rectangle?
A. inches
B. inches
C. inches
D. inches
47. A student uses a solution that contains grams of water to conduct an evaporation experiment.
-At the end of one hour, the amount of water in the solution has decreased by
-At the end of two hours, the amount of water in the solution has decreased by another
Which calculations can be used to determine the amount of water, in grams, remaining the solution at the end of the second hour?
A. Step 1:
Step 2:
Step 3:
Step 4:
B. Step 1:
Step 2:
Step 3:
Step 4:
C. Step 1:
Step 2:
Step 3:
Step 4:
D. Step 1:
Step 2:
Step 3:
Step 4:
50. What is the value of the expression ?
A.
B.
C.
D.
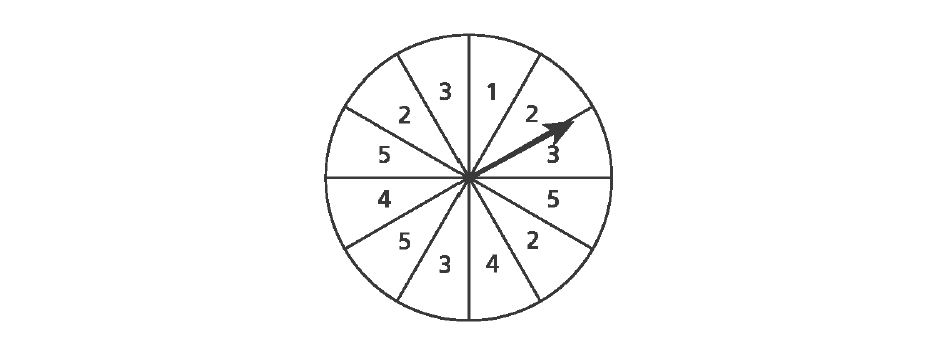
51. A board game has a spinner divided into sections of equal size. Each section is labeled with a number between and
.
Which number is a reasonable estimate of the number of times the spinner will land on a section labeled over the course of
spins?
A.
B.
C.
D.