2017 Grade 6 Math Regents

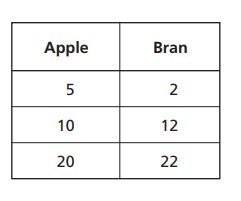
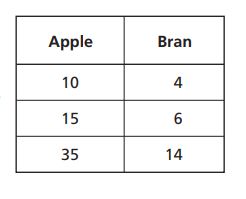
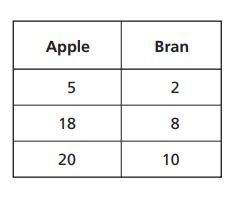
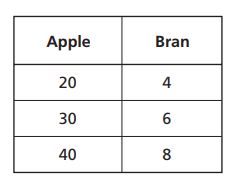
1. A bakery sells $5$ apple muffins for every $2$ bran muffins sold. Which table shows this ratio?

A.
B.
C.
D.

2. In which set do all of the values make the inequality $2x - 1 \textless 10$ true?

A. { $10, 15, 20$ }
B. { $5, 7, 9$ }
C. { $4, 6, 8$ }
D. { $2, 3, 4$ }

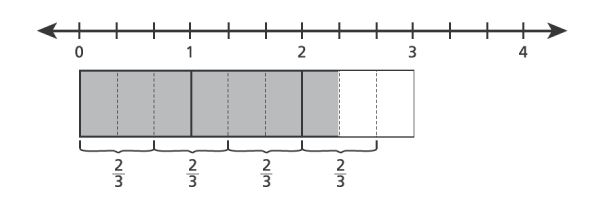
3. The model below reprsents a division problem.

Which equation is represented by the model?

A. $2\dfrac{1}{3} \div \dfrac{2}{3}=3\dfrac{1}{2}$
B. $2\dfrac{1}{3} \div \dfrac{2}{3}=3\dfrac{1}{3}$
C. $\dfrac{7}{1} \div \dfrac{1}{3}=2\dfrac{1}{3}$
D. $\dfrac{2}{3} \div 3\dfrac{1}{2}=2\dfrac{1}{3}$

4. What is the value of the expression below?
$2 [3 (4{2} + 1) ] - 2{3}$

A. $156$
B. $110$
C. $94$
D. $48$

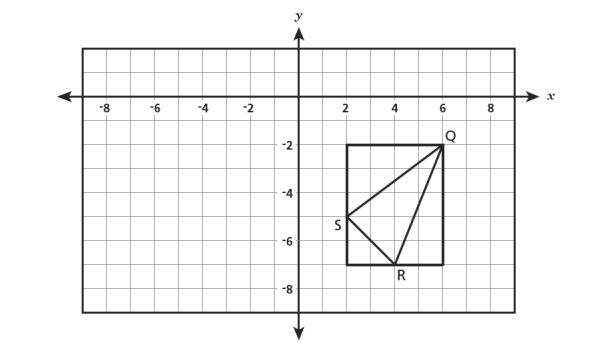
9. Triangle $QRS$ , with vertices $Q(6,-2), R(4,-7)$ , and $S(2,-5)$ , is drawn insie a rectangle, as shown below.

What is the area, in square units, of triangle $QRS$ ?

A. $7$
B. $10$
C. $13$
D. $18$

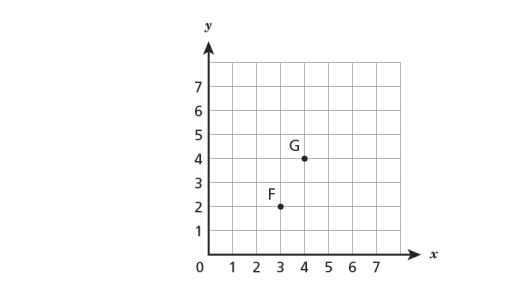
10. Points $F$ and $G$ have been plotted on the coordinate plane below.

Point $G$ and point $H$ are the same distance from point $F$ . Which coordinates could be the location of point $H$ ?

A. ( $1,2$ )
B. ( $4,2$ )
C. ( $5,1$ )
D. ( $2,5$ )

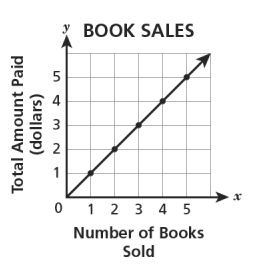
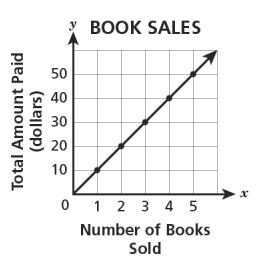
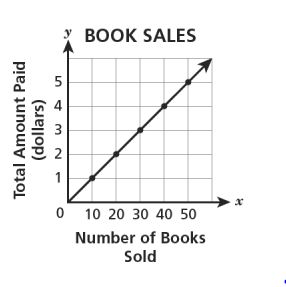
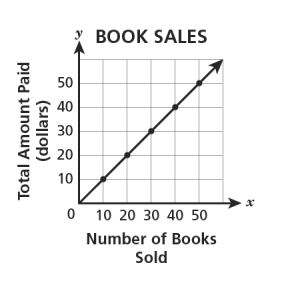
13. A bookstore is selling books for $\$10$ each. Which graph shows the relationship between the number of books, $x$ , the store sold and the total amount of money, $y$ , paid from the book sales?

A.
B.
C.
D.

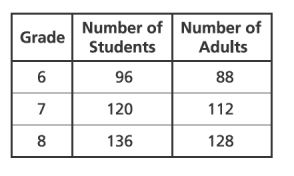
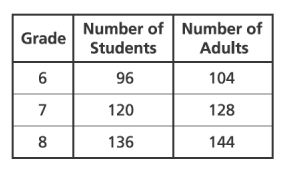
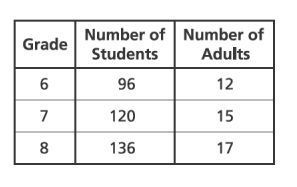
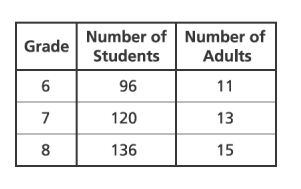
14. The ratio of students to adults on a field trip is $8$ to $1$ . Which table correctly shows this ratio for each grade?

A.
B.
C.
D.

15. Which phrase is a description of $2m + 7$ ?

A. $7$ more than $2$ times $m$
B. $2$ more than $7$ times $m$
C. $2$ times the sum of $7$ and $m$
D. $7$ times the sum of $2$ and $m$

16. George has $\$23$ to spend on art supplies. He wants to buy markers, paper, and glue. If the total cost of the markers and paper is more than $\$14$ , which inequality represents the dollar amount, $p$ , George can spend on glue?

A. $p \textless 9$
B. $p \textgreater 9$
C. $p \textless 37$
D. $p \textgreater 37$

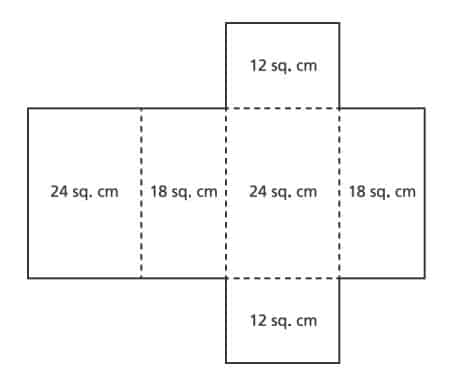
17. The net of a rectangular prism is shown below. The surface area of each face is labeled.

Which values represent the dimensions, in centimeters, of the rectangular prism?

A. $12,18,24$
B. $3,4,8$
C. $3,4,6$
D. $2,9,12$

18. A salesperson had $\$240,000$ in sales last year, which is $60\%$ of the sales she had this year. Which equation could be used to determine $x$ , the salesperson’s total amount of sales, in dollars, for this year?

A. $\dfrac{240,000}{x} = \dfrac{60}{100}$
B. $\dfrac{240,000}{100} = \dfrac{x}{60}$
C. $\dfrac{60}{240,000} = \dfrac{x}{100}$
D. $\dfrac{60}{100} = \dfrac{x}{240,000}$

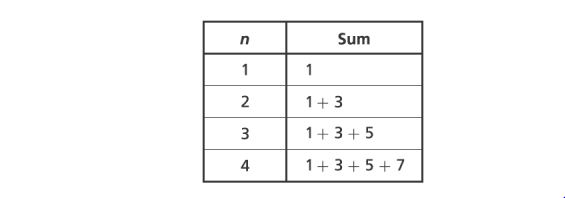
19. A student formed a pattern in which each term is represented by a sum. The first four terms of the pattern are shown below.

Which expression can be used to determine the value of the sum in any term, $n$ ?

A. $n^{2}$
B. $4n$
C. $n + 3$
D. $2^{n}$

20. Jason will use a $\dfrac{1}{3}$ gallon pitcher to fill an empty $\dfrac{3}{4}$ gallon water jug. How much water will he need in order to completely fill the water jug?

A. between $1$ and $2$ full pitchers
B. between $2$ and $3$ full pitchers
C. about $\dfrac{1}{2}$ of a full pitcher
D. about $\dfrac{1}{4}$ of a full pitcher

23. Which expression is equivalent to $5 (6x + 3y)$ ?

A. $11x + 3y$
B. $11x + 8y$
C. $30x + 3y$
D. $30x + 15y$

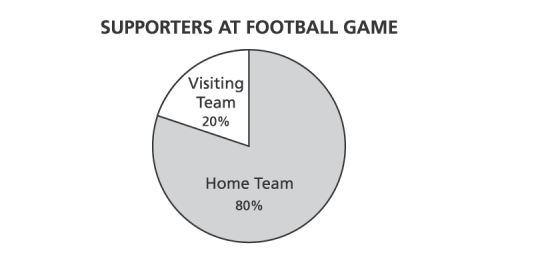
24. The diagram below shows the percentages of people attending a football game who were supporters of either the home team or the visiting team.

If the total number of people attending the game was $64,000$ , how many people were supporters of the home team?

A. $12,800$
B. $38,400$
C. $48,000$
D. $51,200$

25. Which pair of expressions is equivalent for any variable value greater than zero?

A. $3(x + 2)$ and $3x + 2$
B. $4d + 2e$ and $8d + e$
C. $f + f +f + g$ and $3fg$
D. $b + b + 3c$ and $2b + 3c$

26. What is the greatest common factor of $42$ and $84$ ?

A. $7$
B. $21$
C. $42$
D. $84$

27. Kira studied data collected on the school basketball team for one season. She noticed that a player on the team had $13$ successful free throws out of a total of $20$ attempted free throws. To find the percentage of the total free throws attempted by this player that were successful, Kira set up the equivalent ratios below.
$\dfrac{13}{20}=\dfrac{m}{n}$

What are the values for $m$ and $n$ in Kira’s equation?

A. $m=65$ ,
$n=1$
B. $m=100$ ,
$n=65$
C. $m=93$ ,
$n=100$
D. $m=65$ ,
$n=100$

28. What is the least common multiple of $4$ and $10$ ?

A. $14$
B. $20$
C. $40$
D. $60$

29. The surface area, $S$ , of a right rectangular prism with length $l$ , width $w$ , and heigh $h$ can be found using the formula below.
$S=2(lw + wh + hl)$

What is the surface area, in square inches, of a prism with a length of $12$ inches, a width of $9$ inches, and a height of $2$ inches?

A. $300$
B. $258$
C. $150$
D. $92$

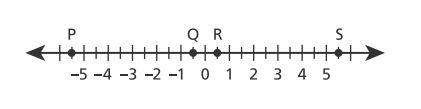
30. Which point on the number line below represents the number opposite the number $-5\dfrac{1}{2}$ ?

A. point $P$
B. point $Q$
C. point $R$
D. point $S$

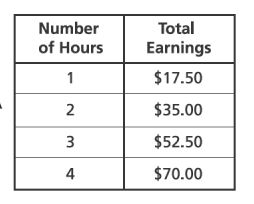
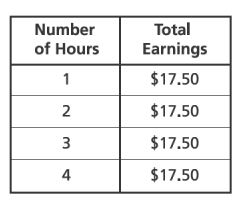
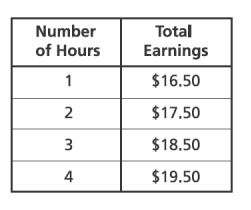
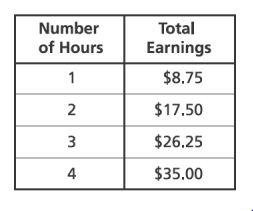
34. In 2010, Kim-Ly earned $ $17.50$ for $2$ hours of work. Which table shows the relationship between the number of hours worked and Kim-ly’s total earnings if her rate per hour is constant?

A.
B.
C.
D.

35. Susan reads a book at a rate of $1$ page every $3$ minutes. If her reading rate remains the same, which method could be used to determine the number of minutes for her to read $18$ pages?

A. add $18$ and $3$
B. divide $18$ by $3$
C. multiply $3$ by $18$
D. subtract $3$ from $18$

36. A triangle has vertices on a coordinate grid at points $J(-1,5), K(4,5)$ , and $L(4,-2)$ . What is the length, in units, of $\overline{KL}$ ?

A. $3$
B. $7$
C. $8$
D. $11$

37. Rosa has a goal of running a total of $100$ miles this month. Each day that she ran, she ran $5$ miles. Which expression could Rosa use to determine how many miles she has left to run after running for $d$ days?

A. $100 - 5d$
B. $5d + 100$
C. $\dfrac{100}{5d}$
D. $5d$

38. The inequality below compares two rational numbers.
$-\dfrac{8}{18}>-\dfrac{17}{27}$

If the two numbers were plotted as values on a horizontal number line, which statement would be true?

A. Both numbers lie to the right of $0$ , and $-\dfrac{8}{18}$ lies to the left of $-\dfrac{17}{18}$ .
B. Both numbers lie to the left of $0$ , and $-\dfrac{8}{18}$ lies to the left of $-\dfrac{17}{27}$ .
C. Both numbers lie to the right of $0$ , and $-\dfrac{8}{18}$ lies to the right of $-\dfrac{17}{27}$ .
D. Both numbers lie to the left $0$ , and $-\dfrac{8}{18}$ lies to the right of $-\dfrac{8}{18}$ lies to the right of $-\dfrac{17}{27}$ .

39. Which value or values for the variable $c$ from the set below will make $5.6 + 0.4c\leq 6c$ true?
{ $0, 0.875, 1, 2.5$ }

A. only $2.5$
B. $1$ and $2.5$
C. $0.875, 1$ , and $2.5$
D. all values in the set

40. Steve ordered plastic cases for storing his baseball cards. Each case has a length of $12$ centimeters, a width of $6.5$ centimeters, and a height of $1.25$ centimeters. What is the volume, in cubic centimeters, of one baseball card case?

A. $39.5$
B. $97.5$
C. $118.5$
D. $202.25$

41. Kim rode her bicycle $135$ miles in $9$ weeks, riding the same distance each week. Eric rode his bicycle $102$ miles in $6$ weeks, riding the same distance each week. Which statement correctly compares the number of miles per week they rode?

A. Eric rode $2$ more miles per week than Kim rode.
B. Kim rode $3$ more miles per week than Eric rode.
C. Kim rode $11$ more miles per week than Eric rode.
D. Eric rode $17$ more miles per week than Kim rode.

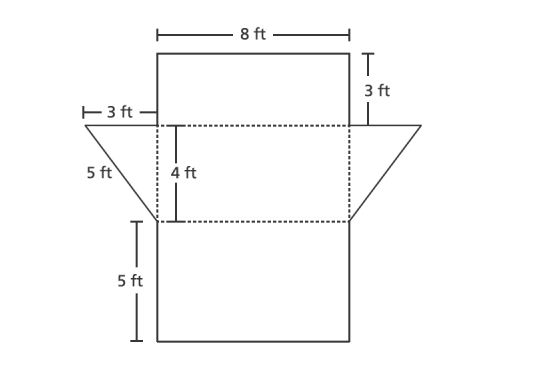
42. A net of a triangular prism is shown below.

What is the surface area, in square feet, of the triangular prism?

A. $44$
B. $96$
C. $108$
D. $120$

43. The two expressions below are equivalent.
$y(2.5 + 7) + y - 2)$ ,
$10.5y - 2$

Which statement best explains why the expressions are equivalent?

A. The expressions have the same value for any value of $y$ .
B. The expressions have the same value for only whole number values of $y$ .
C. The expressions have the same value only when $y$ is an odd number.
D. The expressions have the same value only when $y$ is an even number.

44. Two whole numbers have a least common multiple $60$ .

-Each number is less than or equal to $12$
-The greatest common factor of the two numbers is $2$ .

What are the two numbers?

A. $6$ and $10$
B. $5$ and $12$
C. $10$ and $12$
D. $12$ and $15$

45. Which quantity could go in the blank to make the equation below true?
$x + 2x +$ ___ $=5x$

A. $2$
B. $3$
C. $2x$
D. $3x$

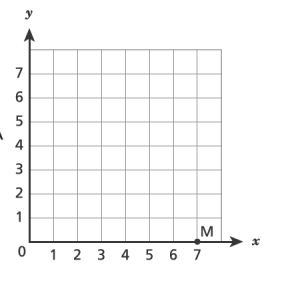
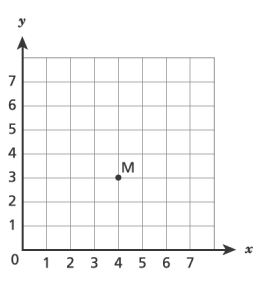
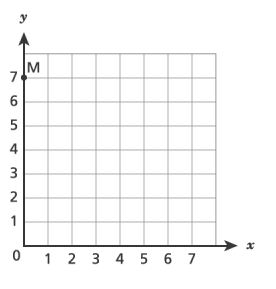
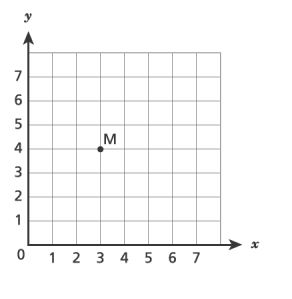
46. Which coordinate grid shows point $M$ plotted at $(4,3)$ ?

A.
B.
C.
D.

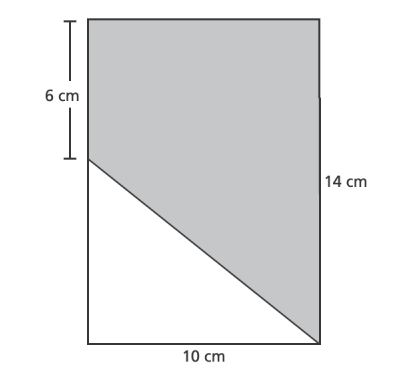
50. What is the area, in square centimeters, of the shaded part of the rectangle shown below?

A. $20$
B. $60$
C. $100$
D. $140$

51. A sandwich shop sells sandwiches for $\$5.95$ each, including tax. The shop received a total of $\$71.40$ from the sales of sandwiches one afternoon. Which equation can be used to determine the number of sandwiches, $x$ , sold by the sandwich shop that afternoon?

A. $5.95 + x=71.40$
B. $5.95 \div 71.40=x$
C. $5.95x = 71.40$
D. $5.95 \div x=71.40$