Table of Contents
Circles
There are a few concepts about circles that will appear on the SAT including area, circumference, equation of a circle, and proportions in circles. Although there are a couple of formulas for circles provided, it is important to review geometry SAT lessons, so you’re prepared for the test.
Basic Formulas
A couple of basic formulas are given on the SAT for circles: area and circumference.
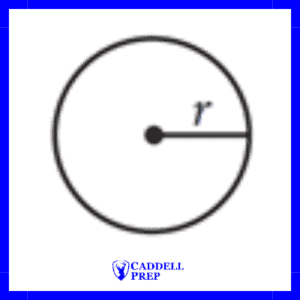
Also, remember that diameter is the width of a circle. It is a chord drawn from one point on the circle to another, passing through the center. It is twice the length of radius, and the radius is half the length of the diameter.
With the two formulas, you will be able to find circumference if you are given the area and vice-versa, because you can find the radius if you are given one.
Example
The circumference of a circle is . What is the area of the circle?
Explanation & Solution
The formula for area of a circle is , so we need to find the radius to find the area.
We are given that the circumference is , so we should use the formula for circumference to find the radius.
,
Divide both sides by , to get
Divide both sides by 2 to get
Now that we know the radius, we can calculate the area.
,
,
Proportions in Circles
Central Angle & Arc Length
The ratio between the central angle and a full circle ( or
radians) is equal to the ratio between the arc length and the full circumference.
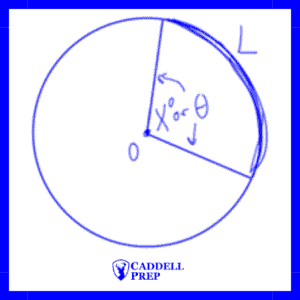
is the central angle in degrees,
represents the arc length, and
is the circumference
is the central angle in degrees,
represents the arc length, and
is the circumference
Central Angle & Sector Area
Also, the ratio between the central angle and a full circle ( or
radians) is equal to the ratio between the sector area and the full area.
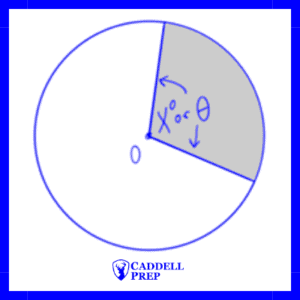
is the central angle in degrees,
represents the arc length, and
is the area
is the central angle in degrees,
represents the arc length, and
is the area
Example
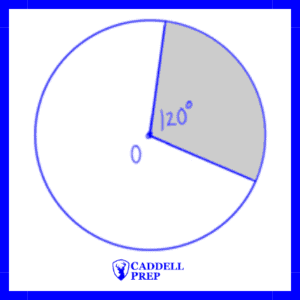
Circle O, shown above, has a radius of 6 inches. What is the area of the shaded portion of the circle?
Explanation & Solution
We have to solve for . However, we need to find the area first, so we can substitute it in for
.
Now, we can substitute the values into the proportion.
,
,
cross-mulitply to get
divide both sides by 360 to get
.
We could have also seen that 120 is one third of the full 260, so the area will be one third of the full area.
Center-Radius Form of the Circle Equation
where the center of the circle is and the radius is
For example, if the center of a circle is and the radius is
, the equation would be
.
If the equation of a circle is , then the center of the circle is
and the radius is
, which could be reduced to
.
Circle Questions with Completing the Square
Sometimes we cannot immediately determine the center and radius of a circle from the equation because it’s not in center-radius form.
For example, if we were given the equation of circle , the center and radius aren’t readily identifiable.
To get the equation in center-radius form, we need to complete the square twice.
First we have to organize the -terms together and
-terms together.
Now, we have to complete the square, by first halving and squaring the coefficients in front of the variables raised to the first power (the coefficients of and
)
,
and
9 will complete the square for the -terms and 1 will complete the square for the
-terms. We have to add the numbers into the equation, but make sure to add them on the right side of the equation also.
,
We can now factor and
. We will end up with the circle equation in center-radius form.
,
,
,
Angles
Naming Angles
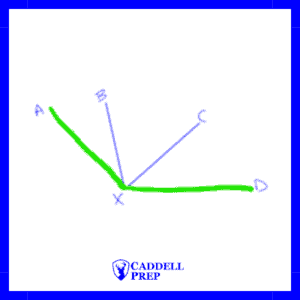
An angle can be named based simply by its vertex or by a point on each of its rays and its vertex, with the vertex in the middle.
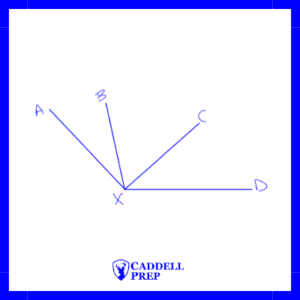
The angle above can be named ∠B, ∠ABC or ∠CBA.
If multiple angles share a vertex, the angles should be named using the vertex and a point on each ray to avoid confusion.
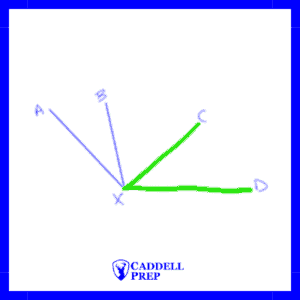
For example, in the diagram below, it would be unclear to refer to any of the angles as ∠X because many angles share X as a vertex.
Here are some of the angles that exist in the diagram above.
∠AXD | ∠AXB | ∠BXC |
∠CXD | ∠AXC | ∠BXD |
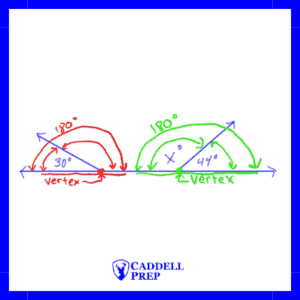
Supplementary Angles
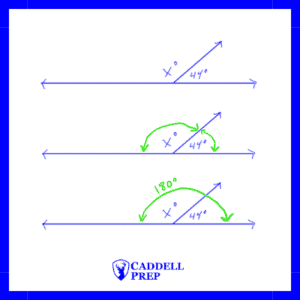
We can set up an equation to solve for .
subtract 44 from both sides
Below is a slightly modified diagram. Another angle with a measurement of is added. What is the value of x now?
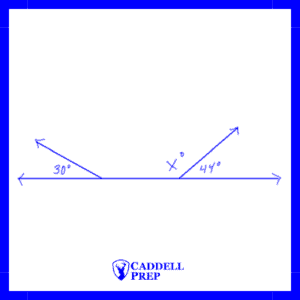
is still
. The angle to the left has no effect on the pair of angles on the right.
Angles combined at a vertex add up to if they form a straight angle.
Refer to the diagram below.