Learn The Absolute Value Inequalities

In this video, we will be learning how to solve Absolute Value Inequalities. Remember to graph your inequalities! After you finish this lesson, view all of our Algebra 1 lessons and practice problems.

When removing absolute value brackets, remember to flip the inequality sign and negate the other side of the inequality!

For Example:

$|2x-8|+8\geq14$

$|2x-8|+8-8\geq14-8\leftarrow$ Subtract 8 from both sides to isolate the quantities in the absolute value brackets

$|2x-8|\geq6\leftarrow$ Now remove the absolute value brackets and separate the equation into 2 cases as shown below

$2x-8\geq6$ $2x-8\leq-6$

$2x-8+8\geq6+8$ $2x-8+8\leq-6+8$

$\frac{2x}{2}\geq\frac{14}{2}$ $\frac{2x}{2}\leq\frac{2}{2}$

$x\geq7$ $x\leq1$

Examples of

Example 1

$2|3x+9|\textless36$

First divide 2 to isolate the quantities in the absolute value brackets
$\dfrac{2|3x+9|}{2}\textless\dfrac{36}{2}$

$|3x+9|\textless18$

Now remove the absolute value brackets and separate the equation into 2 cases

$|3x+9|\textless18$

$3x+9\textless18$ $3x+9\textgreater-18$

$3x+9-9\textless18-9$ $3x+9-9\textgreater-18-9$

$3x\textless9$ $3x\textgreater-27$

$\dfrac{3x}{3}\textless\dfrac{9}{3}$ $\dfrac{3x}{3}\textgreater\dfrac{-27}{3}$

$x\textless3$ $x\textgreater-9$

Example 2

$|2x+5|\geq11$

Remove the absolute value brackets and separate the equation into 2 cases

$|2x+5|\geq11$

$2x+5\geq11$ $2x+5\leq-11$

$2x+5-5\geq11-5$ $2x+5-5\leq-11-5$

$2x\geq6$ $2x\leq-16$

$\dfrac{2x}{6}\geq\dfrac{6}{2}$ $\dfrac{2x}{2}\leq\dfrac{-16}{2}$

$x\geq3$ $x\leq-8$

Video-Lesson Transcript

Let’s go over solving absolute value inequalities.

We’re going to combine our knowledge in solving absolute value equations and solving inequalities.

Let’s look at these:

$\mid m + 5 \mid \textless 3$

Let’s break this down into two:

$m + 5 \textgreater 3$ and $m + 5 \textless -3$

Let’s think about our rule in inequality:

If we multiply or divide by a negative number, we flip the sign.

In the first inequality, we keep the sign because the answer is positive.

In the second inequality, we flip the sign because we’re going to come up with a negative.

Now, let’s solve

$m + 5 - 5 \textgreater 3 - 5$

$m \textgreater -2$

and

$m + 5 - 5 \textless -3 - 5$

$m \textgreater -8$

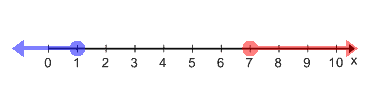
If we graph this, we have a number line that starts with $-8$ and ends with $-2$ .

Draw an open circle at $-2$ and draw a line going to the right since $x$ is greater than $-2$ .

Next, draw an open circle at $-8$ and draw a line going to left.

Their lines don’t meet.

Let’s take a look at

$\mid -10n \mid \textless 10$

Since the absolute value is in itself, we proceed to have two inequalities.

$-10n \textless 10$ and $-10n \textgreater -10$

We flip the sign on the second inequality because we have a negative.

Now let’s solve to get the values of $n$

$\dfrac{-10n}{-10} \textless \dfrac{10}{-10}$

Let’s flip the sign because we’re dividing by a negative number.

$n \textgreater -1$

And let’s do the other one

$-10n \textgreater -10$

$\dfrac{-10n}{-10} \textgreater \dfrac{-10}{-10}$

Again, let’s flip the sign because we’re dividing by a negative number.

$n \textless 1$

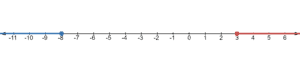
Let’s graph this using a line number which starts at $-1$ and ends with $1$ .

Let’s draw an open circle at $-1$ then draw a line going to the right.

Then let’s draw an open circle at $1$ and then draw a line going to the left.

Here, the lines meet.

This is an example of a conjunction “and”.

While the other is an example of disjunction “or”.

So, a good key to knowing if you’re going to have a conjunction is to look at the original inequality.

If the absolute value in itself has a less than sign, which sort of looks like a letter “c” then it’s going to be a conjunction.

And if not, then it’s going to be a disjunction “or”.

Now, let’s get these two.

$\dfrac{\mid 4x + 1 \mid}{5} \leq 5$

$\mid 2x - 8 \mid + 8 \geq 14$

Let’s solve the first inequality.

$5 \times \dfrac{\mid 4x + 1 \mid}{5} \leq 5\times 5$

$\mid 4x + 1 \mid \leq 25$

Since the absolute value has a less than sign, we know from here that we’ll have a conjunction.

Here, we have two equations:

$4x + 1 \leq 25$ and $4x + 1 \geq -25$

We flipped the sign on the second inequality because we have a negative sign.

Now, let’s solve

$4x + 1 - 1 \leq 25 - 1$

$4x \leq 24$

$dfrac{4x}{4} \leq \dfrac{24}{4}$

$x \leq 6$

And then

$4x + 1 \geq -25$

$4x + 1 - 1 \geq -25 - 1$

$4x \geq -26$

$\dfrac{4x}{4} \geq \dfrac{-26}{4}$

$x \geq {-\dfrac{13}{2}}$

Which we make an improper fraction

$x \geq -6\dfrac{1}{2}$

Let’s graph this by drawing a number line which starts at $-6\dfrac{1}{2}$ and ends with $6$ .

Let’s draw a solid circle at $6$ and a line going to the right.

Then draw a solid circle again at $-6\dfrac{1}{2}$ and a line going to the left.

Two lines met so we have a conjunction.

Let’s try this one

$\mid 2x - 8 \mid + 8 \geq 14$

Let’s get the absolute value by itself by subtracting $8$ on both sides.

$\mid 2x - 8 \mid + 8 - 8 \geq 14 - 8$

$\mid 2x - 8 \mid \geq 6$

Now, we have two inequalities to solve

$2x - 8 \geq 6$ and $2x - 8 \leq -6$

Then let’s solve both

$2x - 8 \geq 6$

$2x - 8 + 8 \geq 6 + 8$

$2x \geq 14$

$\dfrac{2x}{2} \geq \dfrac{14}{2}$

$x \geq 7$

Then the other one. Here we are expecting it to be a disjunction because it’s greater than.

$2x - 8 + 8 \leq -6 + 8$

$2x \leq 2$

$\dfrac{2x}{2} \leq \dfrac{2}{2}$

$x \leq 1$

Let’s graph this by drawing a number line which starts at $1$ and ends at $7$ .

Then draw a solid circle at $7$ and an arrow going to the right which is everything greater than.

Then draw a solid circle, too, at $1$ and an arrow pointing to the left which represents numbers less than.

So as you can see, this example is a disjunction. Same as we expected.